From RL to RLHF
Published:
In light of the widespread adoption of RLHF in large language models (LLMs), this blog is intended to document my study of RLHF, starting from reinforcement learning.
1. 强化学习基础
1.1. 强化学习概述
强化学习(Reinforcement Learning, RL)研究的是智能体如何在一个环境中通过采取行动、获得奖励(或惩罚)来学习最优策略,以实现长期目标的最大化。
强化学习由两部分组成:智能体(agent)和环境(environment)。在强化学习过程中,智能体与环境一直在交互。智能体在环境中获取某个状态(state)后,它会利用该状态输出一个动作(action),然后这个动作会在环境中被执行,环境会根据智能体采取的动作,输出下一个状态以及当前这个动作带来的奖励(reward)。智能体的目的就是尽可能多地从环境中获取奖励。
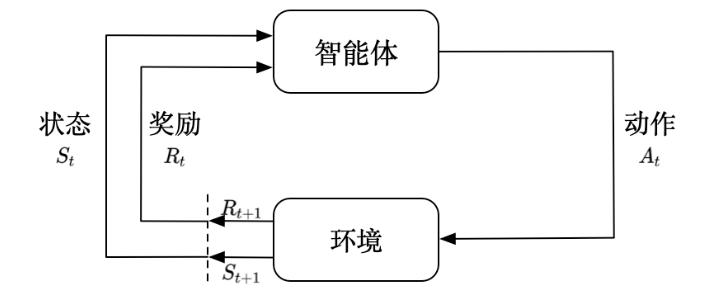
来看一些日常生活中强化学习的例子:(1)股票交易,我们可以不断地买卖股票,然后根据市场给出的反馈来学会怎么去买卖股票才可以让我们的收益最大化。(2)玩雅达利游戏或者其他电脑游戏,我们通过不断试错去探索怎么玩才能通关。
1.2. 为什么需要强化学习
关注强化学习非常重要的一个原因是通过强化学习获得的模型可能超越人类表现。在谈论这一点之前先看看经典的监督学习,我们都知道在大规模图像分类的 ImageNet 数据集上进行预训练得到的 ResNet 模型具备非常强大的视觉表征提取能力,它在当时将图像分类的 SOTA 性能更向前推进了一步。但是,ImageNet 数据集中的数据都是由人类标注得到的,这其实为监督学习的性能制定了一个上限,即监督学习算法的上限就是人类的表现,标注结果决定了它的表现永远不可能超越人类。但是对于强化学习,它在环境里面自己探索,有非常大的潜力,它可以获得超越人类的能力的表现,比如 DeepMind 的 AlphaGo 这样一个强化学习的算法可以把人类顶尖的棋手打败。
相较于监督学习,强化学习的训练更加困难,其主要有以下原因:
- 强化学习通常处理序列数据,样本不满足独立同分布条件:例如在雅达利游戏中下一帧的动作需要输入上一帧数据决定。
- 环境对于智能体状态的奖励存在延迟,使得反馈稀疏不即时,相当于一个“试错”的过程;而监督学习有正确的标签,模型可以通过标签修正自己的预测来即时更新模型。
由此可以总结强化学习的一些基本特征:试错探索、延时稀疏反馈、序列数据。
这里对比一下机器学习中的监督学习、无监督学习和强化学习三大基本范式:
| 特性\范式 | 监督学习 | 无监督学习 | 强化学习 |
|---|---|---|---|
| 监督信号来源 | 人类标注 | 数据内部结构 | 环境反馈 |
| 代表性任务 | 图像分类、语音识别 | 图像聚类、维度压缩 | 机器人控制、游戏博弈 |
| 数据形式 | 数据+标签 | 只有数据 | 状态+动作+奖励序列 |
| 学习目标 | 拟合标签 | 捕捉数据结构 | 最大化累积回报 |
| 反馈时机 | 每个样本即时反馈 | 无外部反馈 | 环境延时反馈 |
1.3. 强化学习基本概念
1.3.1. 序列决策
在强化学习中,智能体一直在与环境进行交互:智能体把它的动作输出给环境,环境取得这个动作后会反馈给智能体一个奖励,并把下一步的观测给与智能体,这一过程称为序列决策过程。从观测出发,将观测、动作和奖励的序列定义为历史:
\[H_t=o_1,a_1,r_1,...,o_t,a_t,r_t.\]基于这些历史信息,环境和智能体会分别通过各自的规则来更新各自的状态,即环境状态 \(S_t^e=f^e(H_t)\),智能体状态 \(S_t^a=f^a(H_t)\)。环境状态是指某一时刻 t 的完整、真实的内部描述,它包含了决定环境未来动态(马尔可夫性)和当前奖励所需的所有信息。智能体状态是指智能体内部维护的、用于决策的、对其所处情境的内部表示。由于智能体往往不可知环境的全局,因此其通过传感器对环境进行感知,在时刻 t 感知到的关于环境的部分、可能有噪声或不完整的信息被称为观测。
当智能体观测与环境状态相同时,即智能体能观测到环境的全部信息,那么称这个环境为完全可观测的,否则称环境为部分可观测的。由于智能体状态的设计目标类似于构建一个关于环境状态的充分统计量,因此在完全可观测下,智能体状态的一个直接选择便是将环境状态设置为自身状态,因此有环境状态=智能体观测=智能体状态。下面介绍动作与奖励。
动作是智能体在环境中做出的行动,在给定的环境中,有效动作的集合经常被称为动作空间。动作空间被分为离散动作空间(机器人只能前后左右走)和连续动作空间(机器人可以360°任意方向走)。
奖励是由环境给的一种标量的反馈信号(scalar feedback signal),这种信号可显示智能体在某一步采取某个策略的表现如何,强化学习的目的就是最大化它的期望长期累积奖励。
1.3.2. 智能体的组成与类型
对于一个强化学习智能体,它可能有一个或多个如下的组成成分。
- 策略(policy):智能体会用策略来选取下一步的动作。
后续主要讨论完全可观测的环境,因此有 \(o_t=s_t\),策略就是智能体将输入变为动作的函数。由于延迟奖励,因此输入只有状态 \(s_t\),输出为动作 \(a_t\)。
策略分为随机性策略与确定性策略。随机项策略输出智能体采取所有可能动作的概率 \(\pi(a\mid s)=p(a_t=a\mid s_t=s)\),确定性策略输出智能体最优可能采取的动作,即 \(a_t=\text{argmax}_a \pi(a\mid s)\)。
强化学习一般使用随机性策略,因为通过引入随机性可以让智能体更好地探索环境。
- 模型(model):模型表示智能体对环境的状态进行理解,它决定了环境中世界的运行方式。
模型决定了下一步的状态,它由状态转移概率和奖励函数两个部分组成。
对于马尔可夫奖励过程,转移概率仅与当前状态有关,即 \(p(s_{t+1}\mid s_t=s)\),奖励为 \(R(s_t)=\mathbb{E}_\pi[r_{t+1}\mid s_t=s]\)。对于马尔可夫决策过程,转移概率与当前状态和动作同时相关,转移概率为 \(p(s_{t+1}\mid s_t=s,a_t=a)\),奖励为 \(R(s_t,a_t)=\mathbb{R}_\pi[r_{t+1}\mid s_t=s,a_t=a]\)。
- 价值函数(value function):我们用价值函数来对当前状态进行评估。价值函数用于评估智能体进入某个状态后,可以对后面的奖励带来多大的影响。价值函数值越大,说明智能体进入这个状态越有利。
价值评估了智能体在某一时刻 t 的状态 \(s_t\) 下的期望长期累积奖励,由于我们更关心近期的奖励,因此引入一个折扣因子 \(\gamma\),价值函数定义为:
\[V_\pi(s)=\mathbb{E}_\pi[G_t\mid s_t=s]=\mathbb{E}_\pi[\sum_{k=0}^{∞} \gamma^k r_{t+k+1}\mid s_t=s].\]其中折扣回报 \(G_t=\sum_{k=0}^{\infin} \gamma^k r_{t+k+1}\) 表示未来某一决策链下的长期累积奖励,下标 \(\pi\) 表示使用策略 \(\pi\) 的时候获得的回报。 \(V_\pi(s)\) 被称为状态价值函数,还有一种动作价值函数 \(Q_\pi(s,a)\),相比 \(V_\pi(s)\),其未来可以取得的累积奖励期望还取决于动作:
\[Q_\pi(s,a)=\mathbb{E}_\pi[G_t\mid s_t=s,a_t=a]=\mathbb{E}_\pi[\sum_{k=0}^{∞} \gamma^k r_{t+k+1}\mid s_t=s,a_t=a].\]根据智能体学习的事物不同,可以把智能体进行归类:
- 基于价值的智能体(Value-based agent),它显式地学习价值函数,隐式地学习它的策略。策略是其从学到的价值函数里面推算出来的。
- 基于策略的智能体(Policy-based agent),直接学习策略,并没有学习价值函数。
- 演员-评论员智能体(Actor-Critic agent),它同时学习策略和价值函数,然后通过两者的交互得到最佳的动作。
2. 马尔可夫决策过程
2.1. 马尔可夫奖励过程
马尔可夫奖励过程(Markov Reward Process, MRP)就是在马尔可夫链的基础上,加上了奖励函数,下面进行介绍。
对于有限步数的 MRP,折扣回报 \(G_t\) 定义为 \(G_t=\sum_{k=0}^{T-t-1} \gamma^{k}r_{t+k+1}\),状态价值函数 \(V(s_t)=\mathbb{E}_\pi[G_t\mid s_t]\)。下面给出贝尔曼方程(Bellman Equation),它刻画了当前状态的价值与未来状态价值之间的联系:
\[V(s_t)=R(s_t)+\gamma \sum_{s_{t+1}} p(s_{t+1}\mid s_t)V(s_{t+1})\]\(R(s_t)=\mathbb{E}[r_{t+1}\mid s_t]\) 为即时回报。下面我们来证明这个等式,首先证明下面这样一个等式:
\[\mathbb{E} [G_{t+1}\mid s_t]=\mathbb{E}[V(s_{t+1})\mid s_t]\]这个等式表明,在给定 t 时刻状态 \(s_t\)下, t+1 时刻的价值期望与折扣回报期望相同。直观上来说,这个等式成立是因为随机变量 \(G_{t+1}\) 的不确定性来自两个方面:①状态 \(s_t\) 转移到状态 \(s_{t+1}\);②状态 \(s_{t+1}\) 之后的随机决策链。第②项的期望即为 \(V(s_{t+1})\),再对第一层求平均即为给定 \(s_t\) 下 \(G_{t+1}\) 的期望。下面用公式证明:
由重期望公式 \(\mathbb{E}[X]=\mathbb{E}[\mathbb{E}[X\mid Y]]\),可以得到 \(\mathbb{E}[X\mid Z]=\mathbb{E}[\mathbb{E}[X\mid Y,Z]\mid Z]\)
\[\begin{aligned} \mathbb{E}[G_{t+1}\mid s_t]&=\mathbb{E}[\mathbb{E}[G_{t+1}\mid s_{t+1},s_t]\mid s_t] \\ &=\mathbb{E}[\mathbb{E}[G_{t+1}\mid s_{t+1}]\mid s_t] \\ &=\mathbb{E}[V(s_{t+1})\mid s_t] \end{aligned}\]继续证明贝尔曼方程:
\[\begin{aligned} V(s_t)&=\mathbb{E}[\sum_{k=0}^{T-t-1} \gamma^k r_{t+k+1}\mid s_t]\\ &=\mathbb{E}[r_{t+1}+\sum_{k=1}^{T-t-1}\gamma^k r_{t+k+1}\mid s_t]\\ &=\mathbb{E}[r_{t+1}\mid s_t]+\gamma \mathbb{E}[G_{t+1}\mid s_t]\\ &=R(s_{t}) +\gamma \mathbb{E}[V(s_{t+1})\mid s_t]\\ &=R(s_{t})+\gamma \sum_{s_{t+1}}p(s_{t+1}\mid s_t) V(s_{t+1}) \end{aligned}\]注:由于 \(r_{t+1},G_{t+1},V(s_{t+1})\) 均为随机变量 \(s_{t+1}\) 的函数,因此上面原始表达式都是对 \(s_{t+1}\) 求期望。
2.2. 马尔可夫决策过程
相较于 MRP,马尔可夫决策过程(Markov Decision Process, MDP)多了决策,在发生状态转移时,未来的状态不仅取决于当前的状态,还依赖于智能体在当前采取的动作,即 \(p(s_{t+1}\mid s_t,a_t)\),奖励函数为 \(R(s_t,a_t)=\mathbb{E}[r_{t+1}\mid s_t,a_t]\),策略为决定智能体当前应当采取什么动作的函数,其被定义为 \(\pi(a_t\mid s_t)=p(a_t\mid s_t)\)。
通过条件概率公式,MDP 可以转化为 MRP,即状态转移与奖励与智能体动作无关:
\[p_\pi(s_{t+1}\mid s_t)=\sum_{a_t}p(s_{t+1}\mid s_t,a_t)\pi(a_t\mid s_t)\\\] \[\begin{aligned} \sum_{a_t}R(s_t,a_t)\pi(a_t\mid s_t)&=\sum_{a_t}\mathbb{E}[r_{t+1}\mid s_t,a_t]\pi(a_t\mid s_t)\\ &=\sum_{a_t}\sum_{s_{t+1}}r_{t+1}p(s_{t+1}\mid s_t,a_t)\pi(a_t\mid s_t)\\ &=\sum_{s_{t+1}}r_{t+1}p(s_{t+1}\mid s_t)\\ &=R(s_t) \end{aligned}\]即:
\[R_\pi(s_t)=\sum_{a_t}R(s_t,a_t)\pi(a_t\mid s_t)\]看完了 MDP 的状态、动作和奖励后,我们来看 MDP 的价值函数。MDP 的状态价值函数定义为 \(V_\pi(s_t)=\mathbb{E}[G_t\mid s_t]\),由于 MDP 还与动作有关,因此引入动作价值函数Q函数 \(Q(s_t,a_t)=\mathbb{E}[G_t\mid s_t,a_t]\)。\(Q(s_t,a_t)\)与 \(V_\pi(s_t)\) 也可以相互转化:
\[V_\pi(s_t)=\sum_{a_t}Q(s_t,a_t)\pi(a_t\mid s_t)\]Q函数的贝尔曼方程给出了当前状态的动作价值与未来状态的状态价值之间的关联:
\[Q(s_t,a_t)=R(s_t,a_t)+\gamma\sum_{s_{t+1}}p(s_{t+1}\mid s_t,a_t)V_\pi(s_{t+1})\]证明:
\[\begin{aligned} Q(s_t,a_t)&=\mathbb{E}[G_t\mid s_t,a_t]\\ &=\mathbb{E}[\sum_{k=0}^{T-t-1}\gamma^k r_{t+k+1}\mid s_t,a_t]\\ &=\mathbb{E}[r_{t+1}\mid s_t,a_t]+\gamma\mathbb{E}[G_{t+1}\mid s_t,a_t]\\ &=R(s_t,a_t)+\gamma \mathbb{E}[V_\pi(s_{t+1})\mid s_t,a_t]\\ &=R(s_t,a_t)+\gamma\sum_{s_{t+1}}p(s_{t+1}\mid s_t,a_t)V_\pi(s_{t+1}) \end{aligned}\]然而,Q函数的贝尔曼方程没有给出当前状态的状态/动作价值与未来状态的状态/动作价值之间的关系。但是这其实并不难,因为组合上面的式子,通过简单变换得到的贝尔曼期望方程就可以给出:
\[\begin{aligned} V_\pi(s_t)&=\sum_{a_t}\pi(a_t\mid s_t)Q(s_t,a_t)\\ &=\sum_{a_t}\pi(a_t\mid s_t)[R(s_t,a_t)+\gamma\sum_{s_{t+1}}p(s_{t+1}\mid s_t,a_t)V_\pi(s_{t+1})] \end{aligned}\] \[\begin{aligned} Q(s_t,a_t)&=R(s_t,a_t)+\gamma\sum_{s_{t+1}}p(s_{t+1}\mid s_t,a_t)V_\pi(s_{t+1})\\ &=R(s_t,a_t)+\gamma\sum_{s_{t+1}}p(s_{t+1}\mid s_t,a_t)\sum_{a_t}\pi(a_{t+1}\mid s_{t+1})Q(s_{t+1},a_{t+1}) \end{aligned}\]上面两式分别为基于状态价值的贝尔曼期望方程和基于动作价值的贝尔曼期望方程。
简单总结一下 MRP 与 MDP:MRP 相较于经典马尔可夫过程多了奖励,MDP 相较于 MRP 多了决策过程。由于多了一个决策,多了一个动作,因此状态转移也多了一个条件,即执行一个动作,导致未来状态的变化,其不仅依赖于当前的状态,也依赖于在当前状态下智能体采取的动作决定的状态变化。对于价值函数,它也多了一个条件,多了一个当前的动作,即当前状态以及采取的动作会决定当前可能得到的奖励的多少。此外,MDP 和 MRP 是可以相互转化的。
最后我们介绍下备份图(backup),它非常清晰直观地展现了 MDP 中 \(Q(s_t,a_t)\) 与 \(V_\pi(s_t)\) 之间的转化关系。
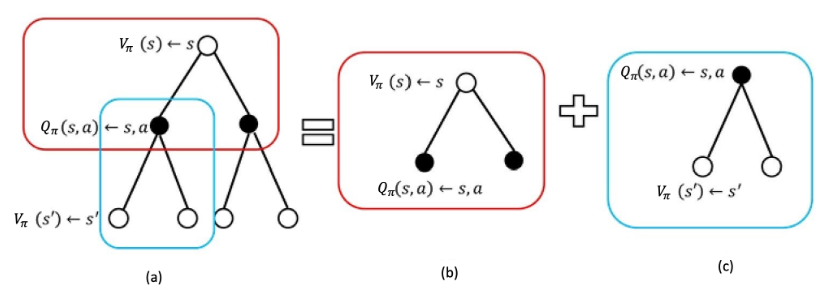
上图展示了 3 种不同的备份图,其中空心节点仅表示状态 \(s\),实心节点表示状态与动作的二元组 \((s,a)\)。每个节点都对应一个价值,即空实心节点分别对应价值 \(V_\pi(s)\) 和 \(Q(s,a)\)。空心节点向实心节点转移表明智能体依据策略 \(\pi(a\mid s)\) 选择了一个动作,实心节点向下一个空心节点转移表明发生了状态转移 \(p(s^{\prime}\mid s,a)\)。在这个备份图中可以清晰看出,MDP 是先有智能体选择动作,再由智能体当前状态和动作共同决定下一时刻状态,而 MRP 直接发生状态转移,而与智能体选择的动作无关。
对于上图 (a),要建立起 \(V_\pi(s)\) 与 \(V_\pi(s^{\prime})\) 之间的联系,首先将价值 \(V_\pi(s^{\prime})\) 对状态 \(s^{\prime}\) 加和,向上备份一层,在动作状态 \((s,a)\) 层再加上即时价值 \(R(s,a)\) 并对动作 \(a\) 进行加和,将价值再向上备份一层,得到:
\[V_\pi(s)=\underbrace{\sum_a\pi(a\mid s)[\underbrace{R(s,a)+\gamma\sum_{s^{\prime}} p(s^{\prime}\mid s,a)V_\pi(s^{\prime})}_{第一层}]}_{第二层}\]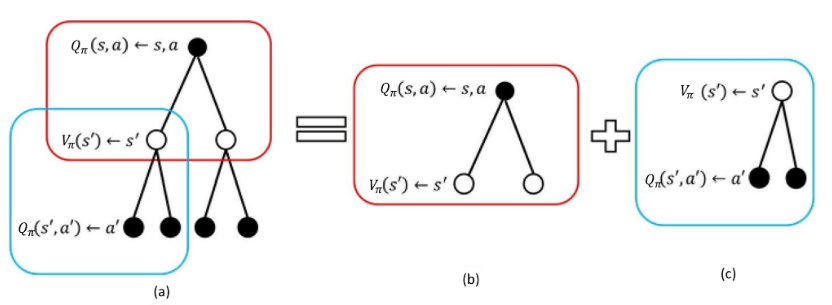
类似地,可以由上面备份图得到 \(Q(s,a)\) 与 \(Q(s^{\prime},a^{\prime})\) 之间的联系:
\[Q(s,a)=\underbrace{R(s,a)+\sum_{s^{\prime}}p(s^{\prime}\mid s,a)\gamma\underbrace{\sum_{a^{\prime}}\pi(a^{\prime}\mid s^{\prime})Q(s^{\prime},a^{\prime}}_{第一层})}_{第二层}\]注:\(s^{\prime}\rightarrow (s,a)\) 要加上即时奖励 \(R(s,a)\),\((s,a)\rightarrow s\) 不需要加即时奖励。
2.3. 马尔可夫决策过程的预测与控制
预测(prediction)和控制(control)是马尔可夫决策过程里面的核心问题。
预测(评估一个给定的策略)的输入是马尔可夫决策过程 \(<S,A,P,R,\gamma>\) 与策略 \(\pi\),输出是价值函数 \(V_\pi\)。预测是指给定一个马尔可夫决策过程以及一个策略 \(\pi\),计算它的价值函数,也就是计算每个状态的价值。
控制(搜索最佳策略)的输入是马尔可夫决策过程 \(<S,A,P,R,\gamma>\) ,输出是最优价值函数 \(V^*\) 与最佳策略 \(\pi^*\)。
2.3.1. 策略评估
策略评估就是给定马尔可夫决策过程和策略,评估我们可以获得多少价值,即对于当前策略,我们可以得到多大的价值,它属于预测的范畴。相邻两个时间 t 和 t+1 的迭代通过贝尔曼期望备份执行:
\[V_\pi^{t+1}(s)=\sum_a\pi(a\mid s)[R(s,a)+\gamma\sum_{s^{\prime}} p(s^{\prime}\mid s,a)V_\pi^{t}(s^{\prime})]\]接下来介绍控制,控制是指在给定马尔可夫决策过程的条件下,寻找最优策略从而得到最优价值函数的方法。对于价值函数 \(V_\pi(s)\),最优价值函数 \(V^*(s)\) 定义为在一种策略下使得每个状态下的状态价值最大的函数,即
\[V^*(s)=\max_\pi V_\pi(s)\]使得每个状态下的状态价值函数 \(V_\pi(s)\) 都最大的策略即为最优策略,即
\[\pi^*(s)=\text{argmax}_{\pi} V_\pi(s)\]可以看出最优策略其实是非常理想的,因为它要求在任意状态下都有最大状态价值,那么这自然引出了一系列问题:最优策略是否存在?最优策略是否唯一?最优策略是随机的还是确定的?如何获得最优策略?这些问题可以通过研究贝尔曼最优方程(Bellman Optimal Equation)来回答。
2.3.2. 贝尔曼最优方程
下面给出贝尔曼最优方程:
\[V^*(s)=\max_{\pi} V_\pi(s)\]将右式展开并改写:
\[\begin{aligned} V_\pi(s)&=\max_\pi \sum_a\pi(a\mid s)[R(s,a)+\gamma\sum_{s^{\prime}} p(s^{\prime}\mid s,a)V_\pi(s^{\prime})]\\ &=\max_\pi \sum_a\pi(a\mid s)Q(s,a) \end{aligned}\]其中智能体模型 \(R(s,a)\) 与 \(p(s^{\prime}\mid s,a)\) 已知,状态价值 \(V_\pi(s)\) 未知。贝尔曼最优方程的向量形式写成
\[V_\pi=\max_\pi (R_\pi+\gamma P_\pi V_\pi)\]对于每个状态,有 \([R_\pi]_s=\sum_a \pi(a\mid s)R(s,a)\),\([P_\pi]_{s,s^{\prime}}=\sum_a\sum_{s^{\prime}} \pi(a\mid s)p(s^{\prime}\mid s,a)\) 。
我们分析一下式子 \(V_\pi(s)=\max_\pi \sum_a \pi(a\mid s)Q(s,a)\) :
\[\begin{aligned} \sum_a \pi(a\mid s)Q(s,a)&\le \sum_a \pi(a\mid s) \max_{a^{\prime}}Q(s,a^{\prime})\\ &\le \max_{a^{\prime}} Q(s,a^{\prime}) \sum_a \pi(a\mid s)\\ &=\max_{a} Q(s,a^{\prime}) \end{aligned}\]可以发现,对于每一个状态 \(s\),我们取使得 Q 函数最大的动作,得到相应的 Q 函数的值是状态价值的一个上界,同时,我们取策略 \(\pi(a\mid s)\) 为
\[\pi(a\mid s)=\left\{ \begin{aligned} 1,\ a=a^{\prime}\\ 0,\ a\neq a^{\prime} \end{aligned} \right.\]就能使上界可达。因此 \(V_\pi(s)=\max_\pi \sum_a\pi(a\mid s)Q(s,a)\ge \max_{a} Q(s,a^{\prime})\) 。总的来说,我们有
\[V_\pi(s)=\max_\pi \sum_a\pi(a\mid s)Q(s,a)=\max_a Q(s,a)\]这一等式表明,最优策略是确定性的、贪婪的,即选择使得 Q 函数 \(Q(s,a)\) 最大的动作的策略。
目前对最优策略有了一个初步的感知,但是由于 Q 函数未知,它并没有提供获得最优策略的方法,并且关于其性质还有待进一步研究,下面进行详细讨论。
我们将贝尔曼最优方程的右侧视作关于 \(V_\pi\) 的函数,那么可以将方程改写为
\[V_\pi=\max_\pi (R_\pi+\gamma P_\pi V_\pi)=f(V_\pi)\]这事实上是一个典型的不动点问题。与之相关的是压缩映射定理:
对于任意具有形式 \(x=f(x)\) 的方程,如果 \(f\) 是一个压缩映射,那么:
I. 存在性:存在一个不动点 \(x^*\) 满足 \(x^*=f(x^*)\)。
II. 唯一性:不动点 \(x^*\) 是唯一的。
III. 算法:考虑一个序列 \(\{x_k\}\) ,其中 \(x_{k+1}=f(x_k)\),那么当 \(k\rightarrow ∞\) 时,\(x_k\rightarrow x^*\)。
其中 \(f\) 是一个压缩映射是指,\(\forall x_1,x_2 \in \mathbb{R}^d\),\(\lVert f(x_1)-f(x_2) \rVert \le \gamma \lVert x_1-x_2 \rVert\),\(\gamma\in (0,1)\)。
可以证明, \(f(V_\pi)\) 中的 \(f\) 是一个压缩映射。这表明对于贝尔曼最优方程 \(V_\pi=\max_\pi (R_\pi+\gamma P_\pi V_\pi)=f(V_\pi)\),总是存在且唯一存在一个不动点 \(V_\pi^*\),并且能通过
\[V_\pi^{k+1}=\max_\pi (R_\pi+\gamma P_\pi V_\pi^k)\]以迭代的形式解出,并且 \(V_\pi^k\rightarrow V_\pi^*\),\(k\rightarrow ∞\)。在获得 \(V_\pi^*\) 后,可以解出最优策略 \(\pi^*\):
\[\pi^*=\text{argmax}_{\pi}(R_\pi+\gamma P_\pi V_\pi^*)\]可以证明,\(\pi^*\) 就是最优策略,且 \(V_{\pi}^*\) 是最优状态价值函数。这个 \(\pi^*\) 就是前面说的,选择使 Q 函数最大的动作的、确定性的、贪婪的策略。此时,
\[V_\pi^*=R_\pi + \gamma P_\pi V_\pi^*\]因此可以说,贝尔曼最优方程是贝尔曼方程的一种特例。
介绍完贝尔曼最优方程,下面介绍价值迭代与策略迭代—两种利用贝尔曼最优方程求解最优策略的 value-based 方法。
2.3.3. 价值迭代
价值迭代(Value Iteration) 就是利用迭代式
\[V_\pi^{k+1}=\max_\pi (R_\pi+\gamma P_\pi V_\pi^k)\]求解最优策略的方法,它分为两个步骤:
Step 1. 策略更新(Policy Update)
\[\begin{aligned} \pi^{k+1}(a\mid s)&=\text{argmax}_\pi \sum_a\pi(a\mid s)[R(s,a)+\gamma\sum_{s^{\prime}} p(s^{\prime}\mid s,a)V_\pi^k(s^{\prime})]\\ &=\text{argmax}_{\pi} \sum_a\pi(a\mid s)Q^k(s,a) \end{aligned}\]从前面的分析可以得知
\[\pi^{k+1}(a\mid s)=\left\{ \begin{aligned} 1,\ a=a^*\\ 0,\ a\neq a^* \end{aligned} \right.\]其中 \(a^*=\text{argmax}_a Q^k(s,a)\) 。
Step 2. 价值更新(Value Update)
由于 \(\pi^{k+1}\) 是贪婪的,所以
\[V^{k+1}(s)=\max_a Q^k(s,a)\]依次逐步向后迭代,直至 \(V^k(s)\) 收敛为止,通过确定性贪婪选取最优策略。
算法流程:
\[V^k(s)\rightarrow Q^k(s,a)\rightarrow \text{greedy policy}\ \pi^k(a\mid s)\rightarrow V^{k+1}(s)=\max_a Q^k(s,a)\rightarrow ...\]2.3.4. 策略迭代
给定一个随机初始化的策略 \(\pi_0\),
Step 1. 策略评估(Policy Evaluation)
由策略 \(\pi_k\) 求出状态价值 \(V^k\)
- 闭式解
- 迭代解(更常用)
Step 2. 策略提升(Policy Improvement)
\[\pi_{k+1}=\text{argmax}_{\pi} (R_\pi + \gamma P_\pi V_\pi^{(n)})\]其中 \(V^{(n)}_\pi\) 为 \(n\) 次内部迭代后得到的价值函数,类似前面每次迭代选取的最优策略利用贪婪得到。可以证明,\(V_{\pi_{k+1}}\ge V_{\pi_k}\) ,即策略每次更新都在不断改进,并最终会收敛到最优解 \(V^*_{\pi}\) 。
算法流程:
\[\pi_0 \rightarrow V_{\pi_0} \rightarrow \pi_1 \rightarrow ...\]价值迭代和策略迭代都是通过优化值函数来间接推导最优策略,而非直接优化策略本身,属于 value-based 方法。
至此,马尔可夫决策过程的内容大体完毕,这一章主要介绍了马尔可夫奖励过程、马尔可夫决策过程、贝尔曼方程以及两种简单 value-based 方法:价值迭代与策略迭代。
3. 策略梯度
在上一章的最后介绍了一些 value-based 方法,即价值迭代与策略迭代,它们基于贝尔曼最优方程,通过逐步提升状态价值函数 \(V_\pi\) 进而间接获得最优策略。本章要介绍的策略梯度属于 policy-based 方法,这种方法将策略参数化为一个网络,并通过梯度提升的方式更新策略网络,以最大化状态价值函数。我们直接来介绍策略梯度定理,经过资料查找,策略梯度定理有一些不同形式,这里仅选取一种与前面内容最为紧密的进行介绍。
3.1. 策略梯度定理
我们将策略定义为一个具有参数 \(\theta\) 的网络 \(\pi_\theta\) ,设初始状态为 \(s_0\),将目标函数 \(J(\theta)\) 定义为在策略 \(\pi_\theta\) 下初始状态为 \(s_0\) 的目标函数:
\[J(\theta)\triangleq V_{\pi_\theta}(s_0)\]我们的目标是最大化 \(J(\theta)\),即最大化初始状态下的状态价值。下面给出策略梯度:
\[\nabla_\theta J(\theta)\propto \mathbb{E}_{s\sim D^{\pi_\theta},a\sim \pi_\theta(a\mid s)} [Q_{\pi_\theta}(s,a)\nabla_\theta \log \pi_\theta(a\mid s)]\]其中 \(D^{\pi_\theta}\) 为归一化后的状态分布。
证明:
\[\begin{aligned} \nabla_\theta J(\theta)&=\nabla_\theta V_{\pi_\theta}(s_0)\\ &=\nabla_\theta[\sum_{a_0} \pi_\theta(a_0\mid s_0)Q_{\pi_\theta}(s_0,a_0)]\\ &=\sum_{a_0}[\nabla_\theta \pi_\theta(a_0\mid s_0)Q_{\pi_\theta}(s_0,a_0)+\pi_\theta(a_0\mid s_0)\nabla_\theta Q_{\pi_\theta}(s_0,a_0)]\\ &=\sum_{a_0}[\nabla_\theta \pi_\theta(a_0\mid s_0)Q_{\pi_\theta}(s_0,a_0)+\pi_\theta(a_0\mid s_0)\nabla_\theta [R(s_0,a_0)+\gamma \sum_{s_1}p(s_1\mid s_0,a_0)V_{\pi_\theta}(s_1)]]\\ &=\sum_{a_0}[\nabla_\theta \pi_\theta(a_0\mid s_0)Q_{\pi_\theta}(s_0,a_0)+\gamma\ \pi_\theta(a_0\mid s_0) \sum_{s_1}p(s_1\mid s_0,a_0) \nabla_\theta V_{\pi_\theta}(s_1)]\\ \end{aligned}\]可以看出求 \(V_{\pi_\theta}(s_0)\) 的梯度涉及到求下一个转移状态 \(s_1\) 的状态价值梯度 \(V_{\pi_\theta}(s_1)\) ,这显然是一个递归的过程。为方便推导,我们记 \(\text{Pr}(s_0\rightarrow x,t,\pi_\theta)\) 为状态 \(s_0\) 在策略 \(\pi_\theta\) 下经过 \(t\) 步转移到状态 \(x\) 的概率,则
\[\text{Pr}(s_0\rightarrow s,0,\pi_\theta)=1 \\ \text{Pr}(s_0\rightarrow s_1,1,\pi_\theta)=\sum_{a_0}\pi_\theta(a_0\mid s_0)p(s_1\mid s_0,a_0)\]记 \(\phi(s)=\sum_a \nabla_\theta \pi_\theta(a\mid s)Q_{\pi_\theta}(s,a)\) ,那么继续往下推:
\[\begin{aligned} \nabla_\theta V_{\pi_\theta}(s_0)&=\phi(s_0)+\gamma \sum_{s_1}\sum_{a_0}\pi_\theta(a_0\mid s_0)p(s_1\mid s_0,a_0)\nabla_\theta V_{\pi_\theta}(s_1)\\ &=\phi(s_0)+\gamma \sum_{s_1}\text{Pr}(s_0\rightarrow s_1,1,\pi_\theta)\nabla_\theta V_{\pi_\theta}(s_1)\\ &=\phi(s_0)+\gamma \sum_{s_1}\text{Pr}(s_0\rightarrow s_1,1,\pi_\theta)[\phi(s_1)+\gamma \sum_{s_2}\text{Pr}(s_1\rightarrow s_2,1,\pi_\theta)\nabla_\theta V_{\pi_\theta}(s_2)]\\ &=\phi(s_0)+\gamma \sum_{s_1}\text{Pr}(s_0\rightarrow s_1,1,\pi_\theta)\phi(s_1)+\gamma^2 \sum_{s_2}\text{Pr}(s_0\rightarrow s_2,2,\pi_\theta)\nabla_\theta V_{\pi_{\theta}}(s_2)\\ &= \cdots\\ &= \sum_{t=0}^{∞} \sum_{s_t} \gamma^t \text{Pr}(s_0\rightarrow s_t,t,\pi_\theta)\phi(s_t) \end{aligned}\]带入 \(\phi(s)\) 的表达式得
\[\begin{aligned} \nabla_\theta V_{\pi_\theta}(s_0)&=\sum_{t=0}^{∞} \sum_{s} \gamma^t \text{Pr}(s_0\rightarrow s_t=s,t,\pi_\theta)[\sum_{a}\nabla_\theta \pi_\theta(a\mid s)Q_{\pi_\theta}(s,a)]\\ &=\sum_{t=0}^{∞} \sum_{s} \gamma^t \text{Pr}(s_0\rightarrow s_t=s,t,\pi_\theta)[\sum_{a}\pi_\theta(a\mid s)[Q_{\pi_\theta}(s,a) \nabla_\theta \log \pi_\theta(a_t\mid s_t)]] \end{aligned}\]记 \(d^{\pi_\theta}(s)=\sum_{t=0}^{∞} \gamma^t \text{Pr}(s_0\rightarrow s_t=s,t,\pi_\theta)\) 为折扣状态分布,由于
\[\begin{aligned} \sum_s d^{\pi_\theta}(s)&=\sum_s \sum_{t=0}^{∞} \gamma^t \text{Pr}(s_0\rightarrow s_t=s,t,\pi_\theta)\\ &=\sum_{t=0}^{∞} \gamma^t\\ &=\frac{1}{1-\gamma} \end{aligned}\]因此它并不是一个标准分布,我们令 \(D^{\pi_\theta}(s)=(1-\gamma) d^{\pi_\theta}(s)\) 将其归一化,那么
\[\begin{aligned} \nabla_\theta V_{\pi_\theta}(s_0)&=\frac{1}{1-\gamma} \sum_s D^{\pi_\theta}(s)[\sum_{a}\pi_\theta(a\mid s)[Q_{\pi_\theta}(s,a) \nabla_\theta \log \pi_\theta(a\mid s)]]\\ &\propto \mathbb{E}_{s\sim D^{\pi_\theta}(s),a\sim \pi_\theta(a\mid s)}[Q_{\pi_\theta}(s,a) \nabla_\theta \log \pi_\theta(a\mid s)] \end{aligned}\]综上,我们有
\[\nabla_\theta J(\theta)\propto \mathbb{E}_{s\sim D^{\pi_\theta},a\sim \pi_\theta(a\mid s)} [Q_{\pi_\theta}(s,a)\nabla_\theta \log \pi_\theta(a\mid s)]\]至此,策略梯度定理证明完毕。从策略梯度中可以看出,\(\nabla_\theta \log \pi_\theta(a\mid s)\) 为对数似然 \(\log \pi_\theta(a\mid s)\) 对 \(\theta\) 的梯度,可以从 \(s\sim D^{\pi_\theta},a\sim \pi_\theta(a\mid s)\) 中采样出一条状态动作组成的轨迹 \(\tau\),那么策略梯度的直观理解就是增大动作价值大的轨迹概率,并降低动作价值小的轨迹概率,最终实现总的状态价值最大化。
实际实现时,我们往往更关心梯度方向而非大小,并且这也可以通过学习率大小来调节,所以成正比而非严格等于是无关紧要的。
从蒙特卡洛的角度看,我们可以先采出 \(N\) 条动作状态轨迹:
\[\tau^0=s_0^0,a_0^0,s_1^0,a_1^0,\cdots \\ \tau^1=s_0^1,a_0^1,s_1^1,a_1^1,\cdots \\ \cdots\]随后进行策略梯度的估计:
\[\nabla_\theta J(\theta)=\frac{1}{N}\sum_{n=0}^N \sum_{t=0}^T Q_{\pi_\theta}(s_t^n,a_t^n)\nabla_\theta \log \pi_\theta(a_t^n\mid s_t^n)\]注意到 \(Q(s_t,a_t)=\mathbb{E}[G_{t}\mid s_t,a_t]=\mathbb{E}[\sum_{k=0}^{T-t-1}\gamma^k r_{t+k+1}\mid s_t,a_t]\),对于单条轨迹, \(Q(s_t,a_t)\) 近似为确定性折扣累积奖励 \(\sum_{k=0}^{T-t-1}\gamma^k r_{t+k+1}\),这其实就是 REINFORCE 算法,REINFORCE 更新 \(\theta\) 的梯度为
\[\nabla_\theta J(\theta)\approx \frac{1}{N}\sum_{n=0}^N \sum_{t=0}^T (\sum_{k=0}^{T-t-1}\gamma^k r_{t+k+1}^n) \nabla_\theta \log \pi_\theta(a_t^n\mid s_t^n)\]REINFORCE 本质上是通过蒙特卡洛方法对 \(Q_{\pi_\theta}\) 实现无偏估计,但缺点是方差高。
3.2. 优势函数
从策略梯度中看出,Q 函数可以被视作一个权重,当某个状态动作的价值为负值时,策略网络更新后会降低该动作的概率,反之亦然。但是,很多场景中的 Q 值都是正值,在理想情况下,采样了足够多足够丰富的动作后也没什么问题,由于概率归一化,Q 值小的动作概率也会降低。但是当这一条件不成立时,高价值的动作可能由于没有被采样到而在网络更新后被降低概率,这是我们不希望看到的。
一个较好做法是添加基线并让 Q 函数减去基线,这个基线一般可以取所有动作价值的期望,这样权重就会有正有负,就可以有效解决上述问题。因为 \(V_\pi(s)=\mathbb{E}_\pi Q(s,a)\) ,所以就可以取状态价值 \(V_\pi(s)\) 为基线。
可以证明,带有 \(V_\pi(s)\) 基线的策略梯度是无偏的(更一般地,带有常数基线都是无偏的),只需证明 \(\mathbb{E}_{s\sim D^{\pi_\theta},a\sim \pi_\theta(a\mid s)} [V_{\pi_\theta}(s)\nabla_\theta \log \pi_\theta(a\mid s)]=0\) :
\[\begin{aligned} \mathbb{E}_{s\sim D^{\pi_\theta},a\sim \pi_\theta(a\mid s)} [V_{\pi_\theta}(s)\nabla_\theta \log \pi_\theta(a\mid s)]&=\sum_s\sum_a D^{\pi_\theta}(s)\pi_\theta(a\mid s)V_{\pi_\theta}(s)\nabla_\theta \log \pi_\theta(a\mid s)\\ &=\sum_s D^{\pi_\theta}(s)V_{\pi_\theta}(s)\sum_a \pi_\theta(a\mid s)\nabla_\theta \log \pi_\theta(a\mid s)\\ &=\sum_s D^{\pi_\theta}(s)V_{\pi_\theta}(s) \nabla_\theta \sum_a \pi_\theta(a\mid s)\\ &=0 \end{aligned}\]基于此,下面引出优势函数
\[A_{\pi_\theta}(s,a)=Q_{\pi_\theta}(s,a)-V_{\pi_\theta}(s)\]优势函数表示在状态 \(s\) 下采取动作 \(a\) 相较于平均动作的价值差异。当 \(A_\pi(s,a)> 0\) 则说明采取的动作 \(a\) 比当前策略下的平均动作更好,当 \(A_\pi(s,a)> 0\) 则说明采取的动作 \(a\) 比当前策略下的平均动作更差。
基于以上分析,我们将 Q 函数换成优势函数,策略梯度近似为
\[\mathbb{E}_{s\sim D^{\pi_\theta},a\sim \pi_\theta(a\mid s)} [A_{\pi_\theta}(s,a)\nabla_\theta \log \pi_\theta(a\mid s)]\]更一般地,将策略梯度写成以下形式
\[\mathbb{E}_{\tau\sim p(\tau)}[\sum_{t=0}^{∞} \Psi_t\nabla_\theta \pi_\theta(a_t\mid s_t)]\]其中 \(\Psi_t\) 可以是以下多种形式:
- \(\sum_{t=0}^{∞} \gamma^t r(s_t,a_t)\) ,表示轨迹的总回报;
- \(\sum_{t^\prime=t}^{∞} \gamma^t r(s_{t^\prime},a_{t^{\prime}})\) ,表示在动作状态 \(s_{t},a_{t}\) 之后的回报;
- \(\sum_{t^\prime=t}^{∞} \gamma^t r(s_{t^\prime},a_{t^{\prime}}) - b(s_{t^\prime})\) ,引入基线函数;
- \(Q_{\pi_\theta}(s_t,a_t)\) ,动作价值函数,直接学习 \(Q\) 网络;
- \(A_{\pi_\theta}(s_t,a_t)\) ,优势函数,同时维护 \(Q\) 网络和 \(V\) 网络;
- \(r(s_t,a_t)+\gamma V_{\pi_\theta}(s_{t+1},a_{t+1})-V_{\pi_\theta}(s_t,a_t)\) ,一步时序差分估计,只需维护 \(V\) 网络。
最后一点会在下一小节详细说明。前三种本质上是利用蒙特卡洛采样方法,是 model-free 的方法,后三种需要利用网络对函数近似,是 model-based 方法。
上述一系列算法被称为 Actor-Critic,其中 actor 表示策略模型 \(\pi_\theta\),critic 表示价值模型 \(\Psi_\phi\),它是 value-based 方法和 policy-based 方法的结合。actor 负责与环境交互采集数据,并在 critic 的指导下利用策略梯度学习一个更好的策略模型;critic 通过 actor 与环境交互产生的数据学习一个价值模型,思想类似策略评估,它负责判断状态与动作的好坏。
3.3. 广义优势估计
在基于优势函数的策略梯度中,需要对 \(A_\pi(s,a)\) 进行估计,REINFORCE 通过 model-free 的蒙特卡洛采样来实现,其特点是低偏差,但可能引入高方差。现在从另一个角度考虑,将优势函数展开:
\[\begin{aligned} A_\pi(s_t,a_t)&=Q_\pi(s_t,a_t)-V_\pi(s_t)\\ &=\mathbb{E}_{s_{t+1}\sim p(s_{t+1}\mid s_t,a_t)}[R(s_t,a_t)+\gamma V_\pi(s_{t+1})]-V_\pi(s_t)\\ &=\mathbb{E}_{s_{t+1}\sim p(s_{t+1}\mid s_t,a_t)}[R(s_t,a_t)+\gamma V_\pi(s_{t+1})-V_\pi(s_t)] \end{aligned}\]于是可以写出一步优势估计:
\[\hat{A}_t^{(1)}:=\delta_t^V=-V_\pi(s_t)+R_t+\gamma V_\pi(s_{t+1})\]其中 \(V_\pi(\cdot)\) 未知,需要进行近似,从而引入了偏差,这可以通过一个网络 \(V_\phi\) 来实现,这个网络又被称为 Critic,策略网络 \(\pi_\theta\) 又被称为 Actor。 这种方式计算高效,无需像蒙特卡洛方法那样等待整个轨迹结束,只需下一状态便可进行估计。为了减小偏差,Shulman 提出了广义优势估计(GAE),它组合了优势函数的多步时序差分。我们继续改写优势函数:
\[\begin{aligned} A_\pi(s_t,a_t)&=Q_\pi(s_t,a_t)-V_\pi(s_t)\\ &=-V_\pi(s_t)+\mathbb{E}[\sum_{k=0}^{T-t-1}\gamma^k r_{t+k+1}\mid s_t,a_t]\\ &=-V_\pi(s_t)+\mathbb{E}[r_{t+1}\mid s_t,a_t]+\gamma\mathbb{E}[r_{t+2}\mid s_t,a_t]+ \gamma^2\mathbb{E}[G_{t+2}\mid s_t,a_t]\\ &=\mathbb{E}[-V_\pi(s_t)+R_{t+1}+\gamma R_{t+2}+ \gamma^2V_\pi(s_{t+2})]\\ \end{aligned}\]所以优势函数 2 步估计为
\[\hat{A}_t^{(2)}:=\delta_t^V+\gamma \delta_{t+1}^V=-V_\pi(s_t)+R_{t+1}+\gamma R_{t+2}+ \gamma^2V_\pi(s_{t+2})\]推广到 k 步估计:
\[\hat{A}_t^{(k)}:=\sum_{l=0}^{k-1}\gamma^l \delta_{t+l}^V=-V_\pi(s_t)+R_{t+1}+\gamma R_{t+2}+ \cdots + \gamma^kV_\pi(s_{t+k})\]估计的步数越多,轨迹越长,偏差越小,方差越大。GAE 指数加权平均了 1 步到无穷步的优势函数估计:
\[\begin{aligned} \hat{A}_t^{GAE(\gamma,\lambda)}&:=(1-\lambda)\hat{A}_t^{(1)}+(1-\lambda)\lambda \hat{A}_t^{(2)}+\cdots\\ &=(1-\lambda)(\delta_t^V+\lambda(\delta_t^V+\gamma \delta_{t+1}^V)+\cdots)\\ &=\sum_{l=0}^{∞}(\gamma \lambda)^l \delta_{t+l}^V\\ &=\sum_{l=0}^{∞}(\gamma \lambda)^l(R_{t+l}+\gamma V_\pi(s_{t+l+1})-V_\pi(s_{t+l})) \end{aligned}\]上面式子第 1 行中第 \(l\) 项的权重为 \((1-\lambda)\lambda^l\) ,这是一个几何分布概率质量函数,它是一个指数衰减的权重,其次对 \(l\) 求和为 \(1\) ,保证了是一个凸组合。从上式可以看出:
当 \(\lambda\) 很小时,1 步估计具有很高的权重,而其余项权重很小,GAE 退化为一步时序差分 \(R_t+\gamma V_\pi(s_{t+1})-V_\pi(s_{t})\) ;
当 \(\lambda\) 接近于 \(1\) 时,后续项依然具有很高权重,GAE 利用整个序列来估计优势。
总的来说,GAE \(\hat{A}_t^{GAE(\gamma,\lambda)}\) 通过控制 \(\lambda\) 很好平衡了偏差与方差,能取得更好的效果,已经被广泛使用。
4. 基于策略的方法
前面铺垫了那么多,终于到了这里。本章开始介绍一些我们常见的算法,包括 TRPO、PPO、DPO、GRPO。
4.1. TRPO
TRPO 全称 “Trust Region Policy Optimization”,即”信赖域策略优化”。它是一个基于策略梯度的算法,于2015年被伯克利的博士生John Schulman提出。
在 TRPO 算法被提出之前,策略梯度算法的问题之一是更新步长的选取。如果步长选取不好,那么优化后的策略就可能变差,在差的策略上采样进行后续优化可能会导致策略网络越来越差,最终导致模型的崩溃。因此,如何选取一个合适的步长对于策略梯度算法至关重要,我们希望在策略更新后,新策略对应的价值函数的值不能更差。那么,一个自然的想法就是尝试将新策略的价值函数分解为旧策略的价值函数与其他项。如果其他项始终不小于 0 ,那么新策略的价值就是一直递增的。
Sham Kakade 于2002年给出了以下等式,它给出了新策略 \(\tilde{\pi}\) 价值与旧策略 \(\pi\) 价值之间的关联:
\[\eta(\tilde{\pi})=\eta(\pi)+\mathbb{E}_{s_0,a_0,\cdots \mid \tilde{\pi}}[\sum_{t=0}^{∞}\gamma^t A_\pi(s_t,a_t)]\]证明:
记 \(\tau=(s_0,a_0,\cdots)\) ,则
\[\begin{aligned} &\mathbb{E}_{\tau \mid \tilde{\pi}}[\sum_{t=0}^{∞}\gamma^t A_\pi(s_t,a_t)]\\ &=\mathbb{E}_{\tau \mid \tilde{\pi}}[\sum_{t=0}^{∞}\gamma^t(r(s_t,a_t)+\gamma V_\pi(s_{t+1})-V_\pi(s_t))]\\ &=\mathbb{E}_{\tau \mid \tilde{\pi}}[\sum_{t=0}^{∞}\gamma^t r(s_t,a_t)+\sum_{t=0}^{∞}\gamma^t(\gamma V_\pi(s_{t+1})-V_\pi(s_t))]\\ &=\mathbb{E}_{\tau \mid \tilde{\pi}}[\sum_{t=0}^{∞}\gamma^t r(s_t,a_t)]+\mathbb{E}_{s_0}[-V_\pi(s_0)]\\ &=\eta(\tilde{\pi})-\eta(\pi) \end{aligned}\]移项即可得
\[\eta(\tilde{\pi})=\eta(\pi)+\mathbb{E}_{s_0,a_0,\cdots \mid \tilde{\pi}}[\sum_{t=0}^{∞}\gamma^t A_\pi(s_t,a_t)]\]我们继续把上式右侧那一项多展开些:
\[\eta(\tilde{\pi})=\eta(\pi)+\sum_{t=0}^{∞}\sum_s p(s_t=s\mid \tilde{\pi})\sum_a \tilde{\pi}(a\mid s)\gamma^t A_\pi(s,a)\]记 \(\rho_{\tilde{\pi}}(s)=\sum_{t=0}^{∞}\gamma^t p(s_t=s\mid \tilde{\pi})\),那么
\[\eta(\tilde{\pi})=\eta(\pi)+\sum_s \rho_{\tilde{\pi}}(s)\sum_a \tilde{\pi}(a\mid s)A_\pi(s,a)\]从上式可以看出,如果在状态 \(s\) 下存在优势 \(A_\pi(s,a)>0\) 的 \(a\),那么在策略更新时只要取到这个动作,就能保证新策略 \(\tilde{\pi}\) 的价值大于旧策略 \(\pi\) 的价值。然而,在实际中优势并不总为正,并且由于此时动作由未知的新策略 \(\tilde{\pi}\) 产生,这导致了难以直接优化 \(\eta(\tilde{\pi})\)。
思考:直接的策略梯度优化方法中,只是给出了旧策略价值的上升方向,但是优化到新策略时,策略发生了变化,估计价值需要重新采样,因此新策略价值不一定好。而上式直接给出了新旧策略价值之间的关系,那么对于需要优化的新策略最大化其价值即可,但是上式右侧又导致了难以优化。
由于目标函数 \(\eta(\tilde{\pi})\) 难以优化,我们考虑 minorization-maximization(MM)算法
MM算法是一种迭代优化方法,它利用函数的凸性来找到它们的最大值或最小值。当目标函数 \(f(\theta)\) 难以优化时,算法不直接对目标函数求最优化解,转而寻求一个易于优化的目标函数 \(g(\theta)\),通过对这个替代函数求解,使得 \(g(\theta)\) 逐渐逼近 \(f(\theta)\) 的最优解。
MM代表“Majorize-Minimization”或“Minorize-Maximization”,取决于所需的优化是最大化还是最小化。
- Majorize-Minimization:每次迭代找到原非凸目标函数的一个上界函数,求上界函数的最小值。
- Minorize-Maximization:每次迭代找到原非凸目标函数的一个下界函数,求下界函数的最大值。
下图是 Minorize-Maximization 的一个形象解释,可以看到,每次 M 函数向极大值点优化,f 函数的值也在逐渐被最大化。
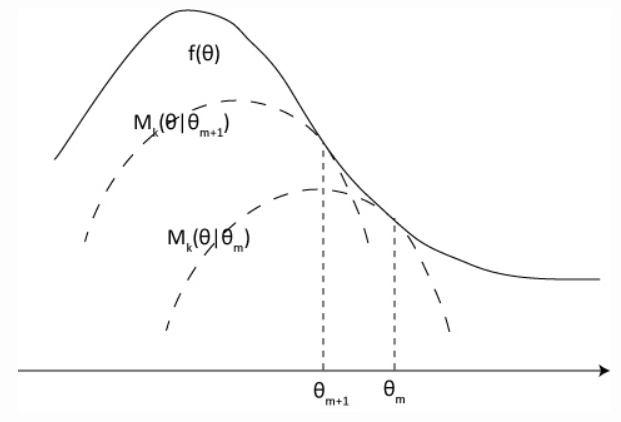
回到正题,TRPO 这篇文章首先考虑忽略状态分布的变化,采取旧策略对应的状态分布,这是因为当新旧参数很接近时,我们将用旧的状态分布代替新的状态分布也是合理的。此时,原来的价值函数变成
\[L_\pi(\tilde{\pi})=\eta(\pi)+\sum_s \rho_{\pi}(s)\sum_a \tilde{\pi}(a\mid s)A_\pi(s,a)\]TRPO 论文后续给出两个重要结论(中间忽略了很多细节,可以去论文查看):
\[L_{\pi_{\theta_0}}(\pi_{\theta_0})=\eta(\pi_{\theta_0}), \ \nabla_\theta L_{\pi_\theta}(\pi_\theta)\mid_{\theta=\theta_0}=\nabla_\theta \eta(\pi_\theta)\mid_{\theta=\theta_0}\] \[\eta(\tilde{\pi})\ge L_\pi(\tilde{\pi})-C\cdot \mathbb{D}_{KL}^{max}(\pi,\tilde{\pi})\]其中 \(\mathbb{D}_{KL}^{max}(\pi,\tilde{\pi}):=\max_s\mathbb{D}_{KL}(\pi(\cdot\mid s),\tilde{\pi}(\cdot\mid s))\) 。设 \(M_i(\pi)=L_{\pi_i}(\pi)-C\cdot \mathbb{D}_{KL}^{max}(\pi_i,\pi)\),那么可以推出:
\[\eta(\pi_{i+1})\ge M_i(\pi_{i+1})\\ \eta(\pi_i)=M_i(\pi_i)\]由 Minorize-Maximization 算法,我们的目标转化为了
\[\max_{\tilde{\pi}} [L_\pi(\tilde{\pi})-C\cdot \mathbb{D}_{KL}^{max}(\tilde{\pi},\pi)]\]注意到 \(\eta(\pi_{i+1})-\eta(\pi_i)\ge M_i(\pi_{i+1})-M_i(\pi_i)\),如果能找到新策略使得 \(M_i(\pi_{i+1})\) 最大,那么
\[\eta(\pi_{i+1})-\eta(\pi_i)\ge M_i(\pi_{i+1})-M_i(\pi_i)\ge 0\]这保证了新策略的价值相对于旧策略价值是提升的,同时也进一步解释了最大化 M 函数的合理性。还没完,为了让这一优化目标更加实用,论文还进行了一些处理。首先是利用重要性采样处理动作分布,对于 \(L_{\pi_{\theta_{old}}}(\pi_\theta)\),其中第一项 \(\eta(\pi_{\theta_{old}})\) 与优化目标无关我们忽略它 ,处理第二项:
\[\begin{aligned} \sum_s \rho_{\pi_{\theta_{old}}}(s)\sum_a\pi_\theta(a\mid s)A_{\pi_{\theta_{old}}}(a,s)&=\sum_s\sum_{t=0}^{∞}\gamma^t p(s_t=s\mid \pi_{\theta_{old}})\sum_a\pi_\theta(a\mid s)A_{\pi_{\theta_{old}}}(a,s)\\ &\approx\sum_{t=0}^{∞}\gamma^t \mathbb{E}_{s\sim \rho_{\pi_{\theta_{old}}}}[\sum_a\pi_\theta(a\mid s)A_{\pi_{\theta_{old}}}(a,s)] \\ &\approx \frac{1}{1-\gamma} \mathbb{E}_{s\sim \rho_{\pi_{\theta_{old}}}}[\sum_a\pi_\theta(a\mid s)A_{\pi_{\theta_{old}}}(a,s)]\\ &=\frac{1}{1-\gamma}\mathbb{E}_{s\sim \rho_{\pi_{\theta_{old}}},a\sim \pi_{\theta_{old}}}[\frac{\pi_\theta(a\mid s)}{\pi_{\theta_{old}}(a\mid s)}A_{\pi_{\theta_{old}}}(a,s)] \end{aligned}\]此外,将原问题转化为带约束的优化问题,并更改 KL 散度的形式,最终 TRPO 的优化目标为:
\[\max_\theta \mathbb{E}_{s\sim \rho_{\pi_{\theta_{old}}},a\sim \pi_{\theta_{old}}}[\frac{\pi_\theta(a\mid s)}{\pi_{\theta_{old}}(a\mid s)}A_{\pi_{\theta_{old}}}(a,s)]\\ s.t.\quad \mathbb{E}_{s\sim \rho_{\pi_{\theta_{old}}}}[\mathbb{D}_{KL}(\pi_{\theta_{old}}(\cdot\mid s),\pi_\theta(\cdot\mid s))]\le \delta\]从优化目标上看,最大化目标要求寻找优势函数大的新策略,而 KL 散度约束项使得新旧策略之间的差异不大,这划定了一个”信任区域”,即在一个”信任区域”上寻找优势函数大的新策略,保持新策略的价值不断提升。
最后说明一下 On-Policy(同策略)与 Off-Policy(异策略)的概念:
- on-policy:训练过程中,模型利用自己的策略与环境交互生成数据,并用这些数据进行模型优化。
- off-policy:训练过程中,模型无需实时生成数据,可以利用预先搜集好或者其他智能体生成的数据进行模型优化。
虽然 TRPO 使用旧模型数据进行优化,但是新旧模型被信任区域限定,相差不算大,依然是 on-policy。
4.2. PPO
PPO 全称 “Proximal Policy Optimization”,即”近端策略优化”,它延续了 TRPO 的核心思想,能保证新策略的价值不断提升。它做了一些小改进使得实现更加简单,其核心思想是限制策略更新的幅度,避免因更新过大导致性能下降。
4.2.1. PPO-penalty
ppo-penalty 将 KL 散度约束项转化为惩罚项以限制策略更新,目标为:
\[\max_\theta \mathbb{E}_{s\sim \rho_{\pi_{\theta_{old}}},a\sim \pi_{\theta_{old}}}[\frac{\pi_\theta(a\mid s)}{\pi_{\theta_{old}}(a\mid s)}A_{\pi_{\theta_{old}}}(a,s)-\beta \ \mathbb{D}_{KL}(\pi_{\theta_{old}}(\cdot\mid s),\pi_\theta(\cdot\mid s))]\]其中 \(\beta\) 依据 KL 散度项的大小动态调整。
4.2.2. PPO-clip
ppo-clip 通过使用裁剪函数限制策略更新的幅度:
\[\max_\theta \mathbb{E}_{s\sim \rho_{\pi_{\theta_{old}}},a\sim \pi_{\theta_{old}}}[\min\{\frac{\pi_\theta(a\mid s)}{\pi_{\theta_{old}}(a\mid s)}A_{\pi_{\theta_{old}}}(a,s),\text{clip}(\frac{\pi_\theta(a\mid s)}{\pi_{\theta_{old}}(a\mid s)},1-\epsilon,1+\epsilon)\cdot A_{\pi_{\theta_{old}}}(a,s) \}]\]\(\text{clip}\) 函数限制了新旧策略的比率 \(\frac{\pi_\theta(a\mid s)}{\pi_{\theta_{old}}(a\mid s)}\) ,即限制了新旧策略的更新幅度。
4.2.3. 与 RLHF 的联系
to be continued
Reference: